Documentation / Generators
Overview of generators
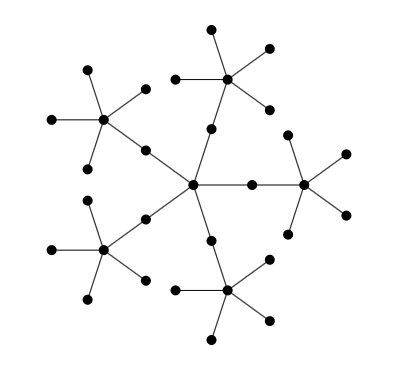
Banana Tree generator.
A (n,k)-banana tree is composed of a root node and n k-stars with one leaf of each star connected to the root node.
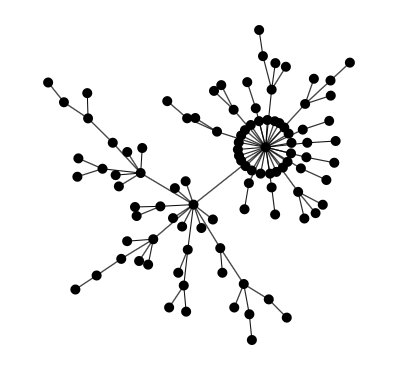
Barabasi-Albert generator
Scale-free graph generator using the preferential attachment rule as defined in the Barabási-Albert model.
This is a very simple graph generator that generates a graph using the preferential attachment rule defined in the Barabási-Albert model: nodes are generated one by one, and each time attached by one or more edges other nodes. The other nodes are chosen using a biased random selection giving more chance to a node if it has a high degree.
:Reference: Albert-László Barabási & Réka Albert, Emergence of scaling in random networks, Science 286: 509–512. October 1999. doi:10.1126/science.286.5439.509.
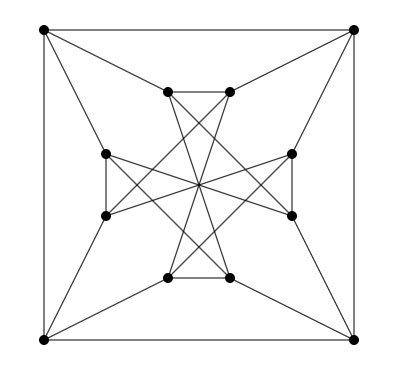
Chvatal graph generator
In the mathematical field of graph theory, the Chvátal graph is an undirected graph with 12 vertices and 24 edges, discovered by Václav Chvátal (1970). It is triangle-free: its girth (the length of its shortest cycle) is four. It is 4-regular: each vertex has exactly four neighbors. And its chromatic number is 4: it can be colored using four colors, but not using only three. It is, as Chvátal observes, the smallest possible 4-chromatic 4-regular triangle-free graph; the only smaller 4-chromatic triangle-free graph is the Grötzsch graph, which has 11 vertices but is not regular.
:Reference: Chvátal, V. (1970), The smallest triangle-free 4-chromatic 4-regular graph, Journal of Combinatorial Theory 9 (1): 93–94, doi:10.1016/S0021-9800(70)80057-6
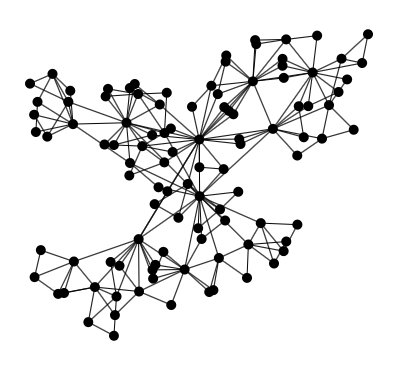
Dorogovtsev-Mendes generator
Generates a graph using the Dorogovtsev - Mendes algorithm. This starts by creating three nodes and tree edges, making a triangle, and then add one node at a time. Each time a node is added, an edge is chosen randomly and the node is connected to the two extremities of this edge.
This process generates a power-low degree distribution, as nodes that have more edges have more chances to be selected since their edges are more represented in the edge set.
This algorithm often generates graphs that seem more suitable than the simple preferential attachment implemented in the PreferentialAttachmentGenerator class (despite the fact more complex and useful preferential attachment generators could be realized in the future).
The Dorogovtsev - Mendes algorithm always produce planar graphs.
The more this generator is iterated, the more nodes are generated. It can therefore generate trees of any size.
:Reference: S. N. Dorogovtsev and J. F. F. Mendes, Evolution of networks, in Adv. Phys, 2002, 1079–1187
Flower Snark generator
In the mathematical field of graph theory, the flower snarks form an infinite family of snarks introduced by Rufus Isaacs in 1975. As snarks, the flower snarks are a connected, bridgeless cubic graphs with chromatic index equal to 4. The flower snarks are non-planar and non-hamiltonian.
:Reference: Isaacs, R. Infinite Families of Nontrivial Trivalent Graphs Which Are Not Tait Colorable. Amer. Math. Monthly 82, 221–239, 1975.
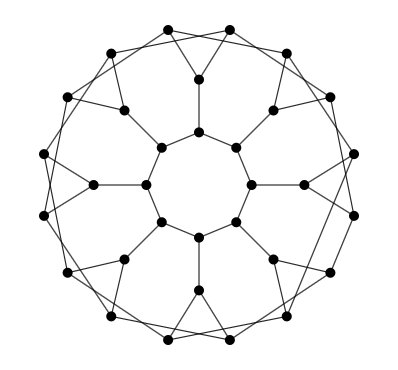
Full connected graph generator
Probably not very useful, still sometimes needed. This generator creates
fully connected graphs of any size. Calling begin() put one unique
node in the graph, then nextEvents() will add a new node each time
it is called.
This generator has the ability to add randomly chosen numerical values on arbitrary attributes on edges or nodes of the graph, and to randomly choose a direction for edges.
A list of attributes can be given for nodes and edges. In this case each new node or edge added will have this attribute and the value will be a randomly chosen number. The range in which these numbers are chosen can be specified.
By default, edges are not oriented. It is possible to ask orientation, in which case the direction is chosen randomly.
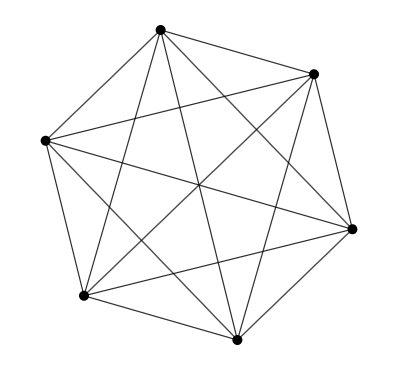
Grid generator
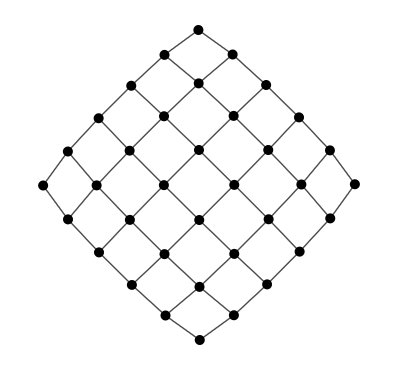
Incomplete grid generator
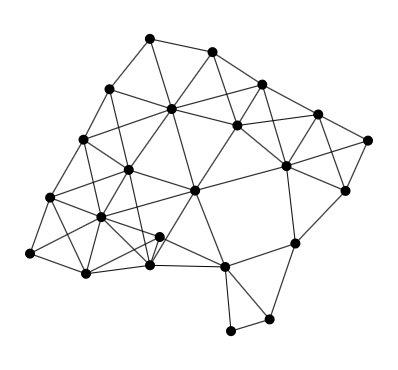
Lobster generator
Lobster are trees where the distance between any node and a root path is less than 2. In this generator, the max distance can be customized.
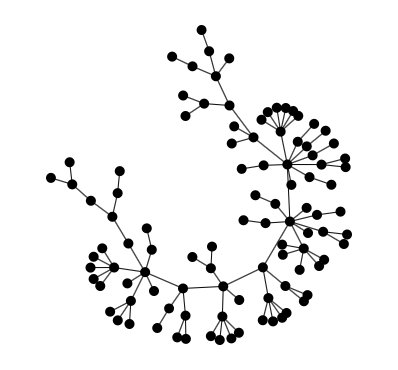
Petersen graph generator
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring. Although the graph is generally credited to Petersen, it had in fact first appeared 12 years earlier, in a paper by A. B. Kempe (1886). Donald Knuth states that the Petersen graph is “a remarkable configuration that serves as a counterexample to many optimistic predictions about what might be true for graphs in general.
:Reference: Petersen, Julius (1898), Sur le théorème de Tait, L’Intermédiaire des Mathématiciens 5: 225–227.
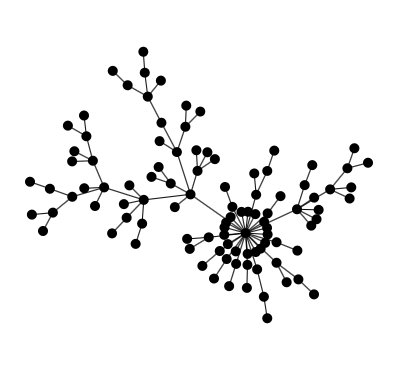
Preferential Attachment generator
Scale-free graph (tree) generator using the preferential attachment rule as defined in the Barabási-Albert model.
This is a very simple graph generator that generates a tree using the preferential attachment rule defined in the Barabási-Albert model: nodes are generated one by one, and each time attached by an edge to another node that has more chance to chosen if it already has lots of nodes attached to it.
The more this generator is iterated, the more nodes are generated. It can therefore generate trees of any size.
:Reference: Albert-László Barabási & Réka Albert Emergence of scaling in random networks. Science 286: 509–512. October 1999. doi:10.1126/science.286.5439.509.
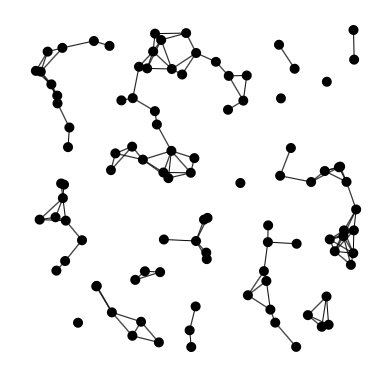
Random Euclidean generator
This generator creates random graphs of any size. Links of such graphs are
created according to a threshold. If the Euclidean distance between two nodes
is less than a given threshold, then a link is created between those 2 nodes.
Calling begin() put one unique node in the graph, then
nextEvents() will add a new node each time it is called and connect
this node to its neighbors according to the threshold planar Euclidean
distance.
This generator has the ability to add randomly chosen numerical values on arbitrary attributes on edges or nodes of the graph, and to randomly choose a direction for edges.
A list of attributes can be given for nodes and edges. In this case each new node or edge added will have this attribute and the value will be a randomly chosen number. The range in which these numbers are chosen can be specified.
By default, edges are not oriented. It is possible to ask orientation, in which case the direction is chosen randomly.
By default, the graph is generated in the plane (2 dimensions) . Cartesian coordinates on nodes will be generated at random. So, each node will automatically be given two attributes: “x” and “y”. If a dimension is specified, then |dimension| attributes are generated, and the 2-norm distance (Euclidean distance) is considered in that dimension between the nodes.
If the dimension is 2, then attributes “x” and “y” are defined for each node. If dimension is 3, then attributes “x”, “y” and “z” are used. For other values of dimension, |dimension| attributes are defined (“xi” with “i” in |dimension|) .
Watts-Strogatz generator
This generator creates small-world graphs of arbitrary size.
This generator is based on the Watts-Strogatz model.
:Reference: Watts, D.J. and Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 393 (6684): 409–10. doi:10.1038/30918. PMID 9623998. 1998.
