Documentation / Generators

Barabàsi-Albert preferential attachement graph generator

Scale-free graph generator using the preferential attachment rule as defined in the Barabási-Albert model.

This is a very simple graph generator that generates a graph using the preferential attachment rule defined in the Barabási-Albert model: nodes are generated one by one, and each time attached by one or more edges other nodes. The other nodes are chosen using a biased random selection giving more chance to a node if it has a high degree.

Usage

The more this generator is iterated, the more nodes are generated. It can therefore generate graphs of any size. One node is generated at each call to nextEvents(). At each node added at least one new edge is added. The number of edges added at each step is given by the getMaxLinksPerStep(). However by default the generator creates a number of edges per new node chosen randomly between 1 and getMaxLinksPerStep(). To have exactly this number of edges at each new node, use setExactlyMaxLinksPerStep(boolean).

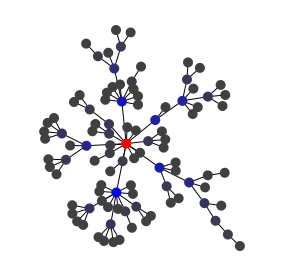
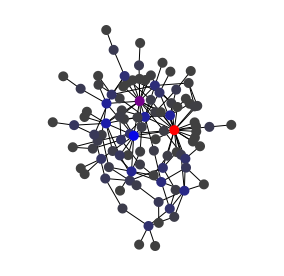
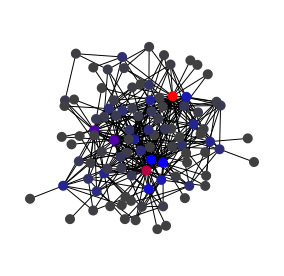
Above are four graphs generated using the Barabàsi-Albert model with four distinct values for the maximum number of links per step, one, two, three and six. Central nodes are highlighted (see the betweenness centrality algorithm).

Complexity

For each new step, the algorithm act in O(n) with n the number of nodes if 1 max edge per new node is created, else the complexity is O(nm) if m max edge per new node is created.

Example

Here is an example of use:

Graph graph = new SingleGraph("Barabàsi-Albert");
// Between 1 and 3 new links per node added.
Generator gen = new BarabasiAlbertGenerator(3);
// Generate 100 nodes:
gen.addSink(graph); 
gen.begin();

for(int i=0; i<100; i++) {
	gen.nextEvents();
}

gen.end();
graph.display();

Reference

• Emergence of scaling in random networks,
• Albert-László Barabási & Réka Albert
• Science 286: 509–512.
• October 1999,
• doi:10.1126/science.286.5439.510