Documentation / Algorithms

A random walk on a graph

Idea

This algorithm create a given number of entities first associated with random nodes in the graph. Then by turns, each entity chooses an edge at random and crosses it. This is iterated a given number of turns. Each time an entity crosses an edge, a count is incremented on it and each time it arrives on a node a count is counted on it.

You can override the entity class to provide your own behaviour for entity movement.

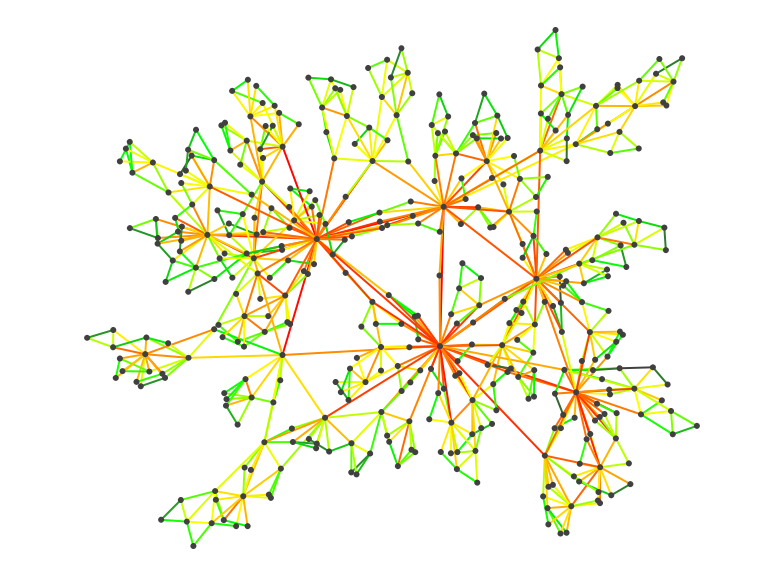
Counts on edges and nodes

If the algorithm was run for an infinite number of turns, each counter would have the same value. However we can choose to stop the algorithm when needed. Furthermore the algorithm can be biased by providing each entity with a memory of the already crossed edges. It can avoid these edges when choosing at random its next edge.

When an entity has no edge to choose (either because of its memory or because it reached a node that is only reachable via a one directed edge), the entity will jump randomly on another node.

When the number of turns awaited is reached, one can observe the counts on each edge and node. Edges and nodes that are very attractive in terms of topology should have a more important count than others.

This algorithm does not cope well with dynamic graphs. You can however improve this by using evaporation. When evaporation is activated, at each turn, the node and edge counts are multiplied by a number between 0 and 1. Therefore each edge or node count must be constantly updated by entities leading to a value that stabilizes in time.

The basic tabu entity

At each step, the default entities move from their current node to another via an edge randomly chosen. This is done in the Entity.step() method.

This method makes a list of all leaving edges of the current node. If the node has no leaving edge, the entity jumps to another randomly chosen node. Then an edge is chosen at random in the list of leaving edges. The edge is chosen uniformly if there are no weights on the edges, else, an edge with an higher weight has more chances to be chosen than an edge with a lower weight.

When crossed, if the memory is larger than 0, the edge crossed is remembered so that the entity will not choose it anew until it crosses as many edges as the memory size.

Usage

With the default entities, you can make a node entirely tabu by putting the tabu attribute on it. No entity will traverse an edge that leads to such a node.

You can change the default entity class either by overriding the createEntity() method or by changing the entity class name using setEntityClass(String).

If the edges have weights, the entities can use them to favour edges with higher weights when randomly choosing them. By default the weights are searched on edges using the weight attribute. However you can override this using setWeightAttribute(String) method.

If you choose to have evaporation on edge counts at each turn, you can set it using setEvaporation(double). The evaporation is a number between 0 and 1. If set to 1 (the default), the counts are not modified, else the counts are multiplied by the evaporation at each turn.

To compute a turn, use the compute() method. This will move each entity from one node to another.

Once computed each edge and node will have an attribute passes stored on it containing the number of passage of an entity. You can change the name of this attribute using setPassesAttribute(String). After each computation of a turn, you can obtain the edge and nodes counts using either the passes attribute, or the utility methods getPasses(Node) and getPasses(Edge).

You can count only the passes on the nodes or edges using the two methods computeEdgesPasses(boolean) and computeNodePasses(boolean).

As some entities may have jumped from their node to another one chosen randomly, you can obtain the number of entities that jumped using getJumpCount().

Complexity

The complexity, at each turn is O(n) with n the number of entities.

Example 1

Here is how to compute a simple pass count for 1000 steps:

Graph graph = new MultiGraph("random walk");
RandomWalk rwalk = new RandomWalk();

// Populate the graph.
rwalk.setEntityCount(graph.getNodeCount()/2);
rwalk.init(graph);

for(int i=0; i<1000; i++) {
	rwalk.compute();
}

rwalk.terminate();

graph.edges().forEach(edge -> {
	System.out.println("Edge %s counts %f%n", edge.getId(), rwalk.getPasses(edge));
});

Example 2

Here is another example where the entities could move indefinitely on the graph using evaporation on the edge counts. To make things more readable, we color the edges according to the count values. The comments explain each step:

    public class TestRandomWalk {
        public void TestRandomWalk() {
    	    Graph graph = new MultiGraph("random walk");
    	    Generator gen   = new DorogovtsevMendesGenerator();
    	    RandomWalk rwalk = new RandomWalk();
    	
            // We generate a 400 nodes Dorogovstev-Mendes graph.
    	    gen.addSink(graph);
    	    gen.begin();
    	    for(int i=0; i<400; i++) {
    		gen.nextEvents();
    	    }
    	    gen.end();
    	
            // We display the graph.
    	    graph.setAttribute("ui.stylesheet", styleSheet);
    	    graph.setAttribute("ui.quality");
    	    graph.setAttribute("ui.antialias");
    	    graph.display();
    	
            // We configure the random walk to use twice as
            // much entities as nodes in the graph. To use
            // a small evaporation on the number of passes
            // per element and a last visited edge list of 
            // 40 elements.
    	    rwalk.setEntityCount(graph.getNodeCount()*2);
    	    rwalk.setEvaporation(0.97);
    	    rwalk.setEntityMemory(40);
    	    rwalk.init(graph);

            // Compute the walks for 3000 steps only as an
            // example, but the test could run forever with
            // a dynamic graph if needed.
    	    for(int i=0; i<3000; i++) {
    	        rwalk.compute();
    	    }
    	    rwalk.terminate();

            // Only when finished we change the edges colors
            // according to the number of passes. This call could
            // be made inside the loop above to show the evolution
            // of the entities passes.
       	    updateGraph(graph, rwalk);

            // We take a small screen-shot of the result.
    	    graph.setAttribute("ui.screenshot", "randomWalk.png");
        }
    
        /**
         * Update the edges with colors corresponding to entities passes.
         */
        public void updateGraph(Graph graph, RandomWalk rwalk) {
            double mine = Double.MAX_VALUE;
    	    double maxe = Double.MIN_VALUE;
    	
            // Obtain the maximum and minimum passes values.
            graph.edges().forEach(edge -> {
			    double passes = rwalk.getPasses(edge);
    	        if(passes>maxe) maxe = passes;
    	        if(passes<mine) mine = passes;
    	    }
    	
            // Set the colors.
			graph.edges().forEach(edge -> {
                double passes = rwalk.getPasses(edge);
    	        double color  = ((passes-mine)/(maxe-mine));
    			edge.setAttribute("ui.color", color);
    	    });
        }
    
        protected static String styleSheet =
    		"edge {"+
    		"	size: 2px;"+
    		"	fill-color: red, yellow, green, #444;"+
    		"	fill-mode: dyn-plain;"+
    		"}"+
    		"node {"+
    		"	size: 6px;"+
    		"	fill-color: #444;"+
    		"}";
    }