Documentation / Algorithms
Betweenness Centrality
Compute the betweenness centrality of each vertex of a given graph.
The betweenness centrality counts how many shortest paths between each pair of nodes of the graph pass by a node. It does it for all nodes of the graph.
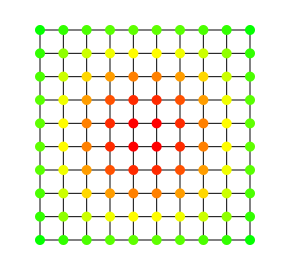
The above graph shows the betweenness centrality applied to a grid graph, where color indicates centrality, green is lower centrality and red is maximal centrality.
Usage
This algorithm, by default, stores the centrality values for each edge inside
the Cb attribute. You can change this attribute name at construction time.
This algorithm does not accept multi-graphs (p-graphs with p>1) yet.
This algorithm does not take into account edge direction yet.
By default the
weight attribute name is weight, you can activate the weights using
setWeighted(). You can change the weight attribute name using the
dedicated constructor or the setWeightAttributeName(String) method.
This method implicitly enable weights in the computation. Use
setUnweighted() to disable weights.
The result of the computation is stored on each node inside the Cb
attribute. You can change the name of this attribute using the dedicated
constructor or the setCentralityAttributeName(String) method.
As the computing of centrality can take a lot of time, you can provide a
progress callback to get notified each time the algorithm finished
processing a node (however the centrality values are usable only when the
algorithm finished). See the registerProgressIndicator(Progress)
method.
Complexity
By default the algorithm performs on a graph considered as not weighted with complexity O(nm). You can specify that the graph edges contain weights in which case the algorithm complexity is O(nm + n^2 log n).
Example
Here is an example of use:
Graph graph = new SingleGraph("Betweenness Test");
// E----D AB=1, BC=5, CD=3, DE=2, BE=6, EA=4
// /| | Cb(A)=4
// / | | Cb(B)=2
// A | | Cb(C)=0
// \ | | Cb(D)=2
// \| | Cb(E)=4
// B----C
Node A = graph.addNode("A");
Node B = graph.addNode("B");
Node E = graph.addNode("E");
Node C = graph.addNode("C");
Node D = graph.addNode("D");
graph.addEdge("AB", "A", "B");
graph.addEdge("BE", "B", "E");
graph.addEdge("BC", "B", "C");
graph.addEdge("ED", "E", "D");
graph.addEdge("CD", "C", "D");
graph.addEdge("AE", "A", "E");
BetweennessCentrality bcb = new BetweennessCentrality();
bcb.setWeightAttributeName("weight");
bcb.setWeight(A, B, 1);
bcb.setWeight(B, E, 6);
bcb.setWeight(B, C, 5);
bcb.setWeight(E, D, 2);
bcb.setWeight(C, D, 3);
bcb.setWeight(A, E, 4);
bcb.init(graph);
bcb.compute();
System.out.println("A="+ A.getAttribute("Cb"));
System.out.println("B="+ B.getAttribute("Cb"));
System.out.println("C="+ C.getAttribute("Cb"));
System.out.println("D="+ D.getAttribute("Cb"));
System.out.println("E="+ E.getAttribute("Cb"));Reference
This is based on the algorithm described in “A Faster Algorithm for Betweenness Centrality”, Ulrik Brandes, Journal of Mathematical Sociology, 2001:
- A Faster Algorithm for Betweenness Centrality,
- Ulrik Brandes,
- Journal of Mathematical Sociology 25:2,
- 2001,
- pp. 163 - 177,
- DOI: 10.1080/0022250X.2001.9990249
And in “On variants of shortest-path betweenness centrality and their generic computation” , of the same author, 2008:
- On variants of shortest-path betweenness centrality and their generic computation,
- Ulrik Brandes,
- Social Networks 30:2,
- pp. 136 - 145,
- 2008,
- issn 0378-8733,
- DOI: 10.1016/j.socnet.2007.11.001